Mechanical ventilators provide critical support for patients who have difficulty breathing or are unable to breathe on their own. They see frequent use in scenarios ranging from routine anesthesia, to neonatal intensive care and life support during the COVID-19 pandemic. A typical ventilator consists of a compressed air source, valves to control the flow of air into and out of the lungs, and a “respiratory circuit” that connects the ventilator to the patient. In some cases, a sedated patient may be connected to the ventilator via a tube inserted through the trachea to their lungs, a process called invasive ventilation.
In both invasive and non-invasive ventilation, the ventilator follows a clinician-prescribed breathing waveform based on a respiratory measurement from the patient (e.g., airway pressure, tidal volume). In order to prevent harm, this demanding task requires both robustness to differences or changes in patients’ lungs and adherence to the desired waveform. Consequently, ventilators require significant attention from highly-trained clinicians in order to ensure that their performance matches the patients’ needs and that they do not cause lung damage.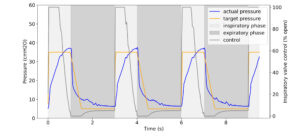
In “Machine Learning for Mechanical Ventilation Control”, we present exploratory research into the design of a deep learning–based algorithm to improve medical ventilator control for invasive ventilation. Using signals from an artificial lung, we design a control algorithm that measures airway pressure and computes necessary adjustments to the airflow to better and more consistently match prescribed values. Compared to other approaches, we demonstrate improved robustness and better performance while requiring less manual intervention from clinicians, which suggests that this approach could reduce the likelihood of harm to a patient’s lungs.
Current Methods
Today, ventilators are controlled with methods belonging to the PID family (i.e., Proportional, Integral, Differential), which control a system based on the history of errors between the observed and desired states. A PID controller uses three characteristics for ventilator control: proportion (“P”) — a comparison of the measured and target pressure; integral (“I”) — the sum of previous measurements; and differential (“D”) — the difference between two previous measurements. Variants of PID have been used since the 17th century and today form the basis of many controllers in both industrial (e.g., controlling heat or fluids) and consumer (e.g., controlling espresso pressure) applications.
PID control forms a solid baseline, relying on the sharp reactivity of P control to rapidly increase lung pressure when breathing in and the stability of I control to hold the breath in before exhaling. However, operators must tune the ventilator for specific patients, often repeatedly, to balance the “ringing” of overzealous P control against the ineffectually slow rise in lung pressure of dominant I control.






